This set of exercises investigates ligation and substituent effects on the energies of the two lowest unoccupied molecular orbitals (the degenerate e_g orbitals) and the two highest occupied molecular orbitals (the nearly degenerate a_1u and a_2u orbitals) of Zn(II) porphyrins.

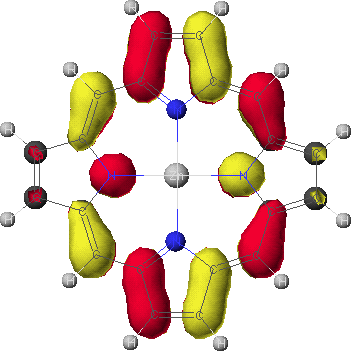
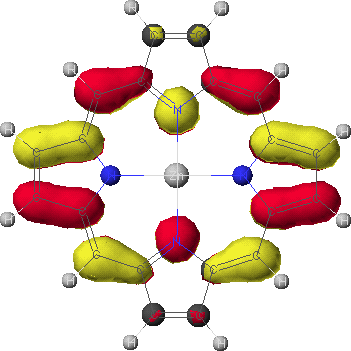
eg	eg
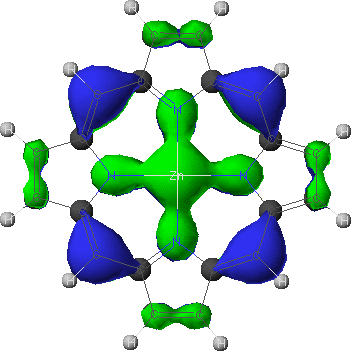
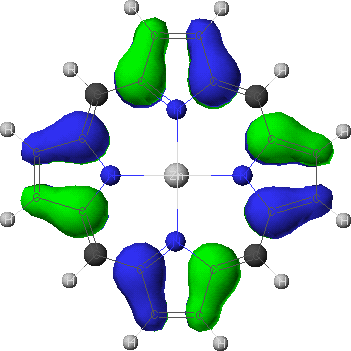
a2u	a1u

The first exercise uses molecular modeling to examine the effect of ligation at the Zn²⁺ ion on the energies of the molecular orbitals of Zn(II) porphine. Knowledge of this effect combined with experimental data on two meso-substituted Zn(II) porphyrins, obtained in the second exercise, permits determination of which of the two occupied orbitals, a_1u or a_2u, is higher in energy in these porphyrins. In the third exercise, the effect of electron-withdrawing substituents at the b-carbons on the reduction potential of Zn(II) porphyrins is investigated through examination of the LUMO energies.

1. Molecular Modeling to Determine the Effect of Ligation on the Orbital Energies in Zn(II) Porphine.
   1. 1. In the Cache Editor, draw Zn(II) porphine as shown above. Instead of starting from scratch, you can modify the structure of heme found in the Fragment library. To call up heme, click on Fragment Tool in the Tool menu and then select Fragment library in the Fragment menu. You will find heme in the porphyrin category. (Note that you do not have to use coordinate bonds and you don't have to put charges on any of the atoms. You will probably have lone pairs on two of the nitrogens.) Once you have the structure of Zn(II) porphine, you can select Geometry under Beautify. Do not select comprehensive, as it will seriously distort the porphyrin.

   2. You will now optimize the structure using a two step approach; molecular mechanics followed by semiempirical mechanics. Select Mechanics under the Applications menu, and, using the following settings, run the calculation.
      

      Then select ZINDO under Applications and run the calculation using the following settings.

      

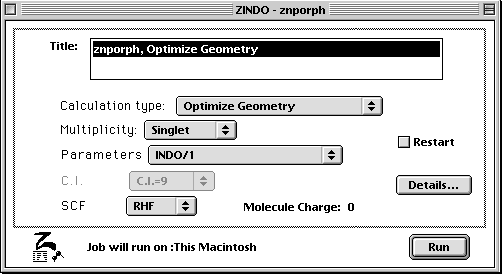
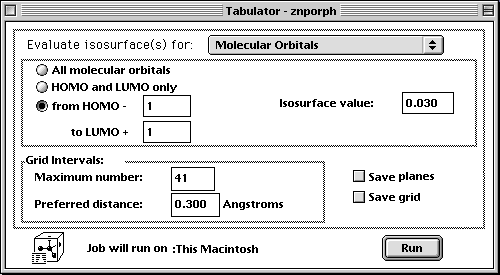
   3. Once the geometry is optimized, the porphyrin should appear flat. You will then calculate the orbitals using the Tabulator under the Applications menu. Be sure to set the isosurface value to 0.030 in order to better view the orbitals. With the settings below, you will calculate the HOMO-1, HOMO, LUMO, and LUMO+1 orbitals.
      

   4. To view the orbitals and determine their energies, go into the Visualizer + from the Applications menu. Once your molecule is displayed, go to the File menu, and select Open Surface. Select one of the four calculated orbitals (identified by a .MO## suffix) by double-clicking on the file name. To see the energy of the orbital, go to View and select Surface Labels. Identify the orbital as a_2u, a_1u, or e_g and write down its energy. Do this for all four orbitals.

   5. Go back to the Cache Editor by selecting Editor from the Applications menu. Open the file with your Zn(II) porphine and add a pyridine molecule as a ligand on the Zn²⁺ ion. Again Beautify using Geometry. Follow steps 2-4 for the ligated Zn(II) porphine.
      

   6. Compare the energies of the orbitals for the ligated and unligated forms of Zn(II) porphine. Which orbital shows the greatest change in energy upon ligation? Rationalize this in terms of the electron-donating nature of the ligand and the shapes of the orbitals.

2. Experiment to Determine the Relative Energies of the a_1u and a_2u orbitals in Meso-Substituted Zn(II) Porphyrins.

   The lowest energy excited singlet states of porphyrins can be thought of as being formed from the molecular orbitals you examined above. An excited singlet state with an a_1ue_g configuration is formed by promoting an electron from the a_1u orbital to an e_g orbital. Likewise, an excited singlet state with an a_2ue_g configuration is formed by promoting an electron from the a_2u orbital to an e_g orbital. These excited singlet states mix to two new singlet states that are nearly 50:50 mixtures of the unmixed states. The closer in energy the unmixed states, the greater the degree of mixing.

   An electronic transition to the higher energy mixed state, the S2 state, is strongly allowed, whereas an electronic transition to the lower energy mixed state, the S1 state, is only weakly allowed. The band in the uv-vis absorption spectrum due to a transition to the S2 state is the Soret band, and the band due to a transition to the vibrationless S1 state is the a band. The greater the degree of mixing, the less intense the a band relative to the Soret band.

   In the experimental uv-vis spectrum, there is also a vibronic band, the b band, that appears at slightly lower wavelengths than the a band. The b band is due to transitions to higher vibrational levels in the S1 state and serves as a "normalization band" in porphyrin absorption spectra. As a result, the intensity of the a band relative to the b band can serve as a measure of how close in energy the a_2u and a_1u orbitals are. For example, if the a_2u and a_1u orbitals have essentially the same energy, the degree of mixing will be large, the a intensity will be small, and, therefore, the a/b intensity ratio will be small. On the other hand, if the a_2u and a_1u orbitals are well separated in energy, the degree of mixing will be smaller, and the a/b intensity ratio will be larger.

   Imagine that the highest occupied molecular orbital of an unligated Zn(II) porphyrin is a_2u. You should have found from the above calculation that ligation at the Zn²⁺ ion will cause the energy of the a_2u orbital to increase. Ignoring the smaller energy changes found for the other orbitals upon ligation, one can surmise that ligation will cause the energy difference between the a_1u and a_2u orbitals to increase and, therefore, the

   a/b intensity ratio to increase. Likewise, if the a_1u orbital is higher in energy in the unligated porphyrin, ligation will cause the a/b intensity ratio to decrease.

   1. Obtain uv-vis absorption spectra of Zn(II) tetraphenylporphyrin, ZnTPP, and Zn(II) tetrakis(pentafluorophenyl) porphyrin, ZnTFPP in neat toluene and, also, in a solution that is 5% pyridine in toluene by volume. Toluene is a nonligating solvent. Use concentrations that make the absorbance values for the a and b bands less than one but high enough to be accurately measured. In other words, you don't want the peaks to be noisy. You might want to subtract a baseline value. The a and b bands should appear in the 500-700 nm region.

   2. From the absorbance values at the a and b peak maxima, determine the a/b intensity ratio. Based upon how this ratio changes upon ligation, state whether the a_1u and a_2u orbital is higher in energy in each of the two Zn(II) porphyrins.

   3. Rationalize your results in terms of the expected electron-donating and electron-withdrawing properties of the meso-substituents (phenyl and pentafluorophenyl) and the shapes of the orbitals.

   4. Unlike the singlet states, the triplet states with a_1ue_g and a_2ue_g configurations do not mix. These states are formed by the same electron promotions that formed the singlet states, but there is a change in the spin of one of the electrons so that there are two unpaired electrons. From your results so far, identify the configuration of the lowest energy triplet state, the T1 state, of ZnTPP and ZnTFPP.

3. Molecular Modeling to Determine the Effect of b-Substitution on the Reduction Potential of Zn(II) Porphines.

   The reduction potential of a molecule correlates with the energy of the LUMO. The lower the LUMO energy, the higher the reduction potential.

   1. Modify the structure of Zn(II) porphine that you made before by replacing the hydrogen atoms at all of the eight b-carbons (two per pyrrole) with, in one case, F atoms and, in the other case, CN groups. For each octa-substituted porphyrin, calculate the energies of the e_g orbitals. (The two e_g orbitals for each molecule should have very close to the same energy.)

   2. From your results, state how the addition of the electron-withdrawing substituents affects the reduction potential. Which porphyrin is easiest to reduce?